¿Por qué el océano se mantiene pegado a la Tierra?
¿Por qué el océano se mantiene pegado a la Tierra a medida que ésta rota? Porque 1600 km/h NO es tan rápido como tú crees.
La velocidad de rotación de la Tierra en el ecuador es de aproximadamente 1600 kilómetros por hora. Esta velocidad suena muy alta, no? Pero alta respecto a qué? Sin duda es alta respecto a la velocidad a la que caminamos (1.4 metros por segundo o 5 kilómetros por hora). No suena tan alta comparada con la velocidad promedio de un avión comercial (un Boeing 777 alcanza velocidades crucero de 900 kilómetros por hora), y sin duda es baja comparada con la velocidad de un Lockheed SR-71 Blackbird, que alcanza velocidades de 3500 kilómetros por hora. Cuando uno habla de una velocidad “alta”, esto sólo tiene sentido un términos relativos.
Entonces ¿es 1600 km/h una velocidad alta?
Un punto de referencia adecuado es la velocidad a la cual que la Tierra podría potencialmente rotar. La Tierra sólo puede rotar a una velocidad máxima; más rápido y se comienza a desarmar. En efecto, a tales velocidades, los océanos serían puestos en órbita. ¿Qué determina este máximo?
Veamos a continuación…
Velocidad de escape y pozos de potencial
Como lo explica de forma excelente esta publicación de xkcd, los planetas tienen un pozo de potencial gravitacional. Mientras más profundo este pozo (es decir, mientras más masa tienen los planetas o más cerca estamos de ellos), más difícil es escapar de su gravedad. A mayor profundidad (o mayor energía gravitacional), uno necesita más energía de movimiento (energía cinética) para escapar de la atracción del planeta. Entonces, la ecuación de esta competencia es sencilla: energía gravitacional versus energía cinética. Los cohetes que son lanzados al espacio necesitan alcanzar cierto nivel de velocidad para poder competir con la atracción del planeta. Esta velocidad, llamada velocidad de escape es: \begin{align} v_{\rm escape}=\sqrt{\frac{2GM_{\rm Tierra}}{R_{\rm Tierra}}}\approx 40000~ {\rm km/h} \end{align} Lo que es casi 30 veces mayor que la velocidad de rotación de la superficie terrestre.
Esta competencia entre el pozo de potencial y la energía de movimiento tiene una analogía con una juguera (licuadora) que funciona a varias velocidades (ver figura abajo).
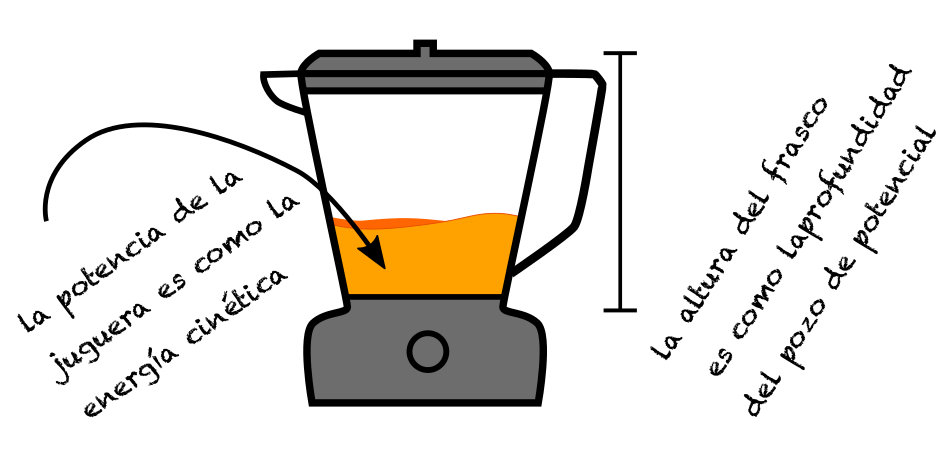
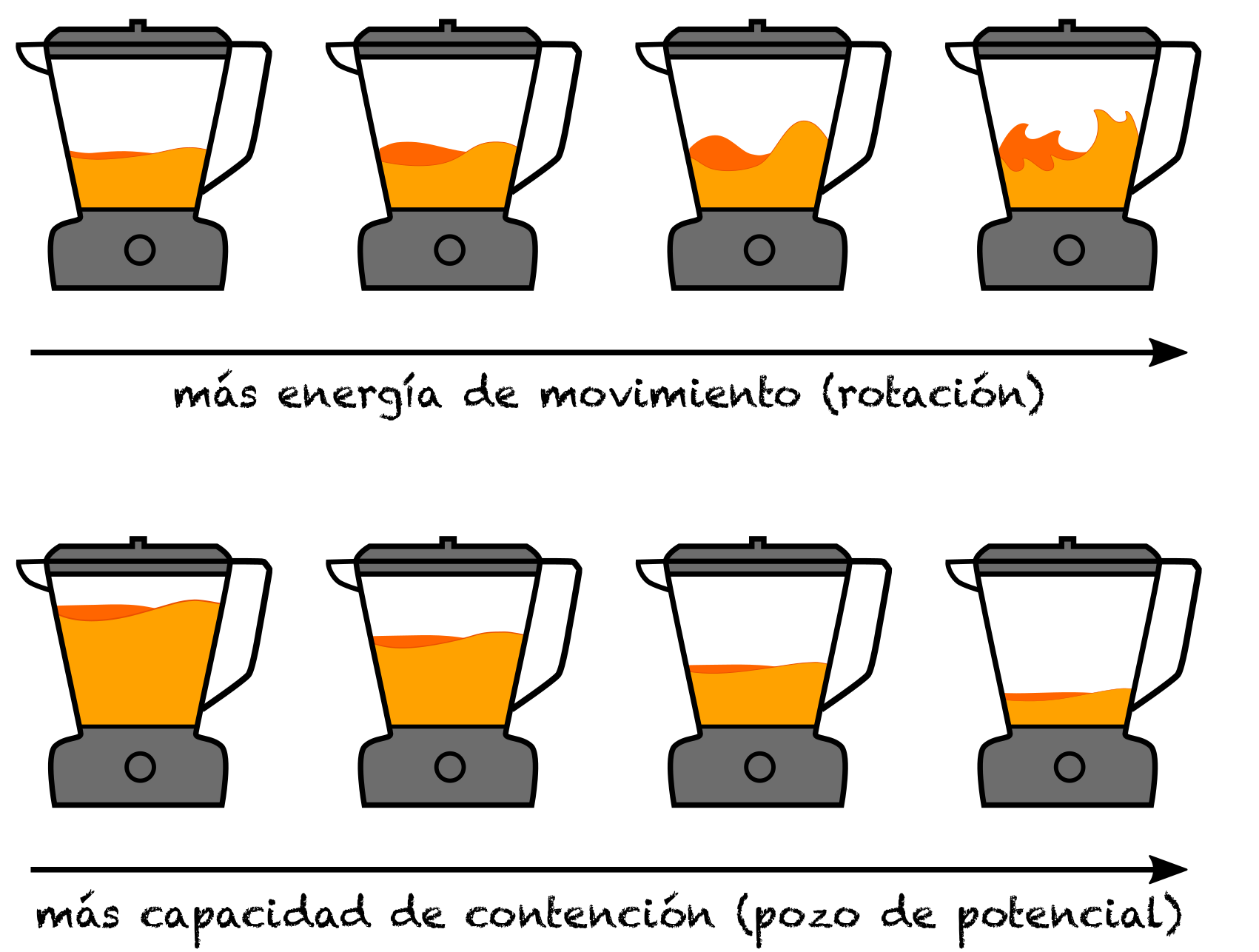
Si la juguera es muy grande (o digamos, el frasco muy alto), no es necesario usar la tapa. Alternativamente, si ésta está funcionando a bajas revoluciones, tampoco es necesario taparla. Es sólo cuando la energía cinética (revoluciones) empieza a competir con el pozo de potencial (altura del frasco) que necesitamos usar la tapa. Ilustramos esto en el esquema siguiente
Algo similar pasa con los océanos de la Tierra. La velocidad de rotación está tan por debajo de la velocidad de escape que el agua no tiene a dónde irse.
Sin embargo, la historia podría ser distinta si la Tierra rotara, digamos, 17 veces más rápido. En ese caso, la distribución de los océanos en la Tierra sería muy distinta, el agua se empezaría a concentrar en el ecuador y parte de ella saldría disparada al espacio.
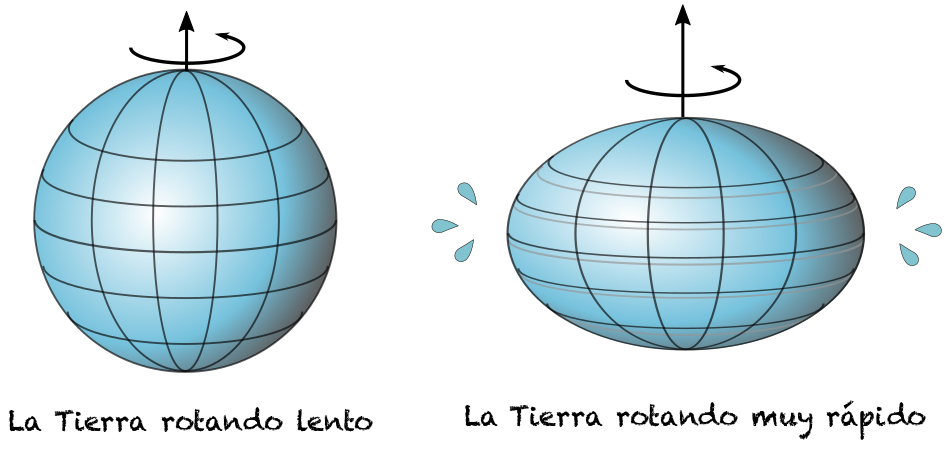
A continuación, mostramos cómo calcular qué tan rápido debe rotar la Tierra para que esto pase.
Velocidad de ruptura
Cualquier objeto unido por la gravedad (la Tierra, otro planeta o una estrella) tiene un propiedad conocido como la “velocidad de ruptura”. Si el objeto rota más rápido que este límite, el éste se desarma. El período de rotación al límite de ruptura es: \begin{align} P_{\rm ruptura}=2\pi\sqrt{\frac{R^3}{GM}} \end{align} En el caso de la Tierra, \(P_{\rm ruptura}\approx1.4~\) horas, es decir, 17 veces más rápido que el período de rotación actual.
Simplemente, la Tierra rota demasiado lento como para poder lanzar sus océanos volando por el espacio. Para poder lograr aquello, el día tendría que durar alrededor de una sola hora en lugar de 24.
Estrellas que rotan rápido
La física de deformación rotacional es aplicable tanto a planetas coma a estrellas. De hecho, la geometría de una esfera de fluido deformada por la rotación se puede calcular exactamente (los detalles los dejamos para otro post). Esta forma se conoce como esferoide oblato.
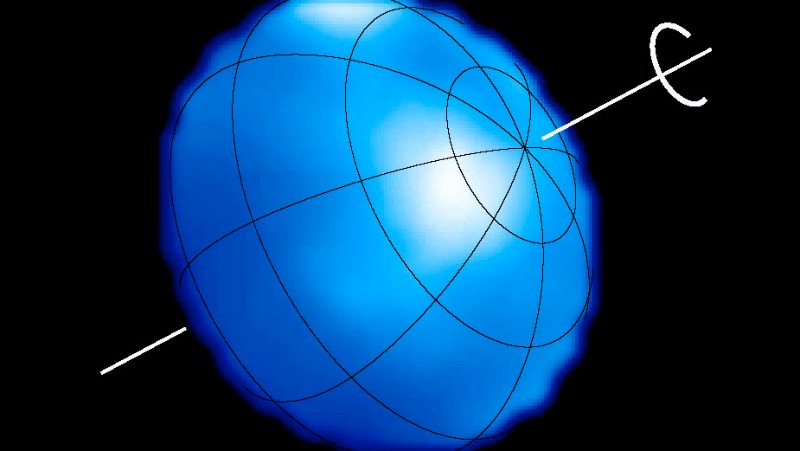
Una de las estrellas que más rápido rota es Altair (la estrella más brillante en la constelación del Aguila y que se puede ver durante el invierno en Chile). Esta estrella rota tan rápido que su deformación se ha medido directamente (ver Monnier et al (2007)) usando una técnica de observación conocida como interferometría. La siguiente figura corresponde a tal medición.
El período de rotación correspondiente a esta deformación es de 8.9 horas! (como referencia, el Sol rota cada 24 días). Esta tasa de rotación corresponde a 290 kilómetros por hora en el ecuador de la estrella. Para una estrella como Altair, el período de rotación al límite de ruptura es \(P_{\rm ruptura}\approx~\)6 horas, es decir, solamente \(30\%\) más rápido que s= rotación real. Altair rota tan rápido que está cerca de desarmarse!