Chicago a la Distancia
La ciudad de Chicago puede verse a grandes distancias debido a sus altos edificios y la escasa topografía de la zona. Incluso se puede ver desde Michigan City, al otro lado del enorme Lago Michigan.
La siguiente es una foto reciente de Chicago (dominio público) vista desde el Sureste. En ella se pueden ver los rascacielos más emblemáticos, como la torre Sears (ahora se llama Willis) a la izquierda de la foto.

Otra toma similar, pero de noche, es la siguiente:

Ambas fotos está tomadas desde el planetario Adler, ubicado en las coordenadas 41°51′59″N (latitud) 87°36′24″W(longitud). Por comparación, las coordenadas de la torre Sears son 41°52′44″N (latitud) 87°38′09″W (longitud). La observación desde el sureste es relevante porque es la misma dirección (a grandes rasgos) que la de Michigan City, la cual discutiremos en detalle más abajo.
Objetos detrás del horizonte
Primero, expliquemos cómo se ven los rascacielos a grandes distancias. En lo siguiente, usaremos algunas de las cosas que aprendimos en un post anterior. Necesitamos recordar dos cosas: (1) que el tamaño aparente (o tamaño angular) de un objeto disminuye con la distancia, y (2) que la distancia al horizonte depende de la altura del nivel de los ojos. El único concepto novedoso, es que objetos detrás del horizonte sí pueden ser visibles. Para ejemplificar, usemos la siguiente figura:
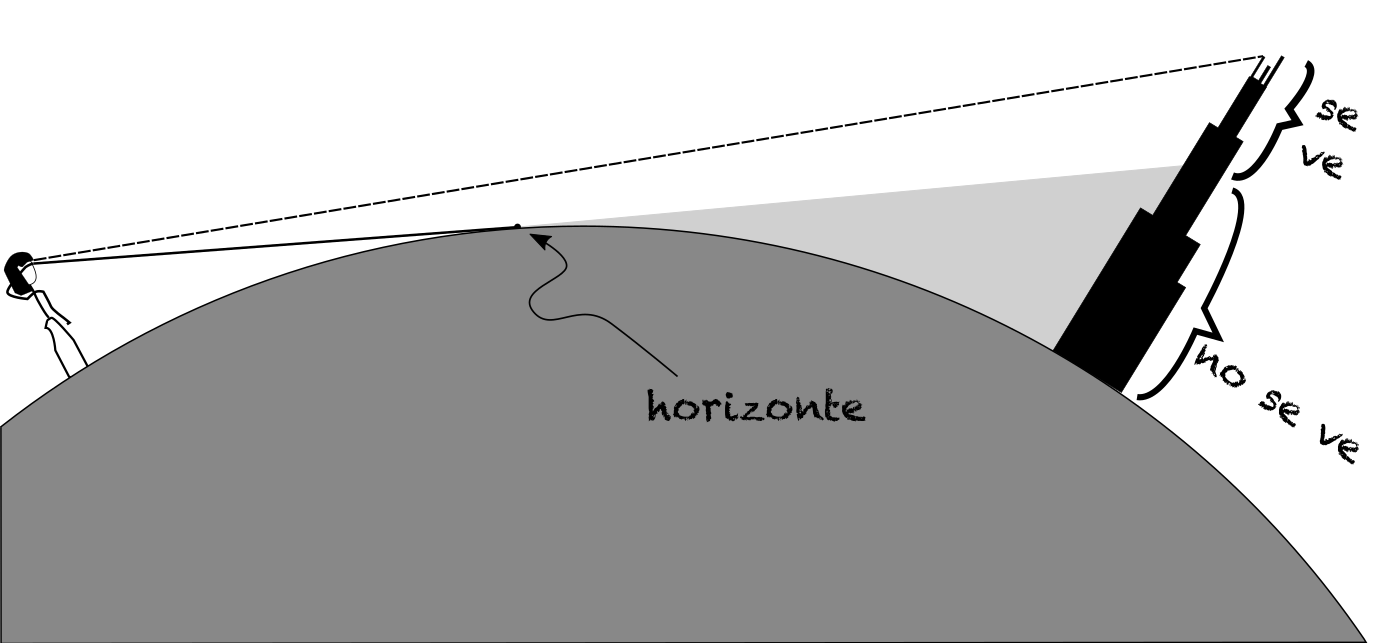
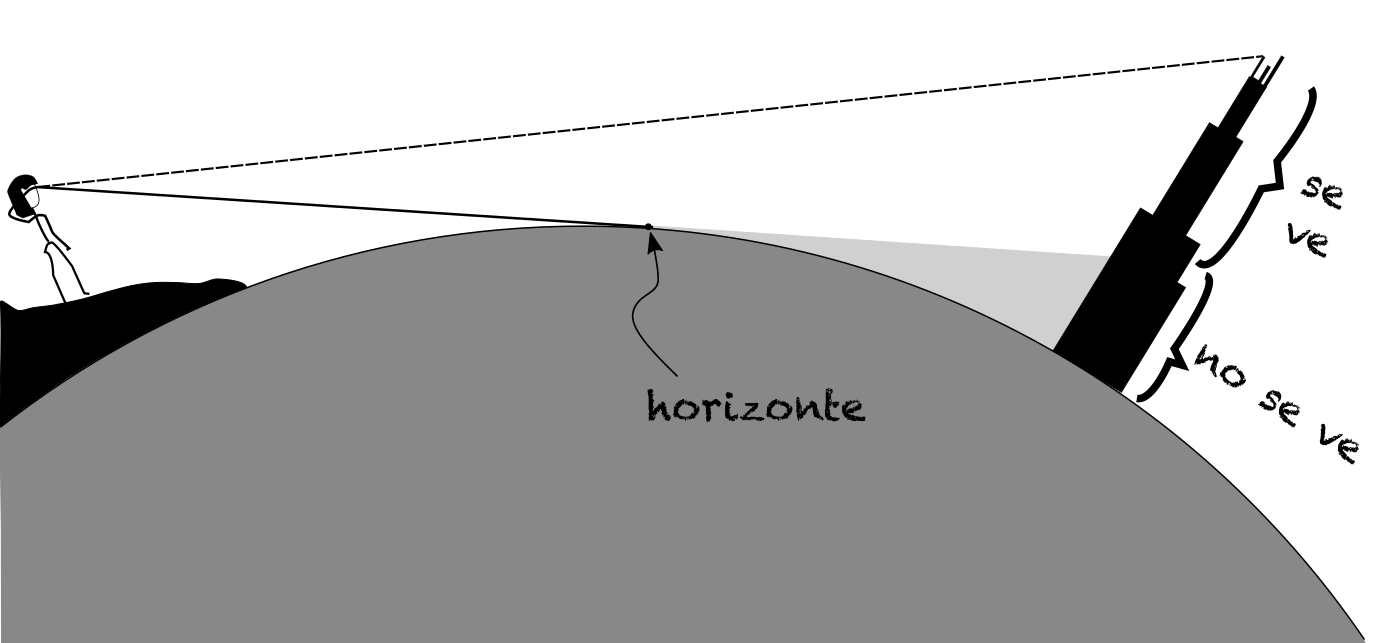
En este caso, el horizonte – según el observador de la izquierda – se encuentra a menor distancia que el edificio. Sin embargo, el edificio se puede ver. En este caso, la Tierra misma es un obstáculo que bloquea (parcialmente) la observación del edificio. Notemos que si el observador está ubicado a una altura mayor que que el radio promedio terrestre (sobre una loma u otro edificio), éste podrá ver una porción mayor del edificio de la derecha. Esta sutileza es importante porque, cuando comparemos con fotos reales, la altura de la cámara determina la fracción de los edificios que se pueden ver.
La fracción de los edificios bloqueada por el horizonte
(Atención: esta sección contiene cálculos. Si prefieres saltarte los detalles, continua en la sección siguiente)
Ahora, veamos con más atención la geometría del observador y el edificio que esta detrás del horizonte:
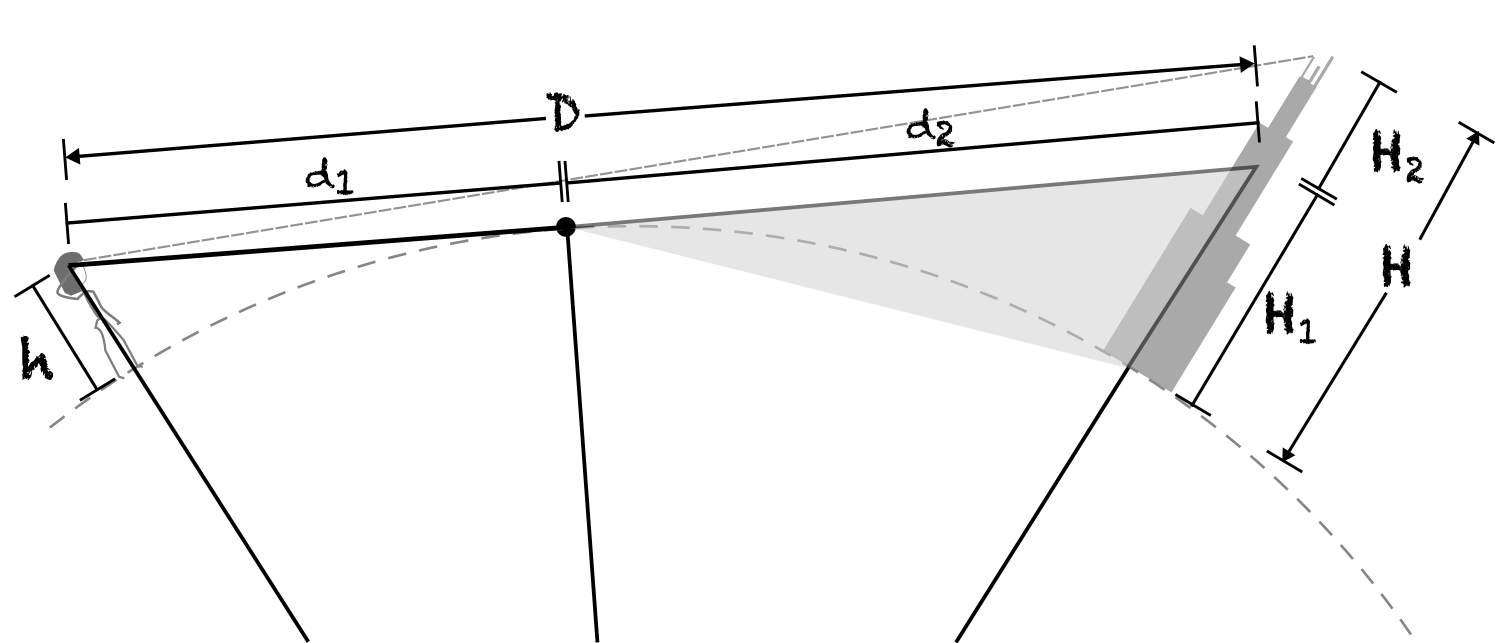
Al igual que antes, la geometría de la observación está descrita por triángulos rectángulos
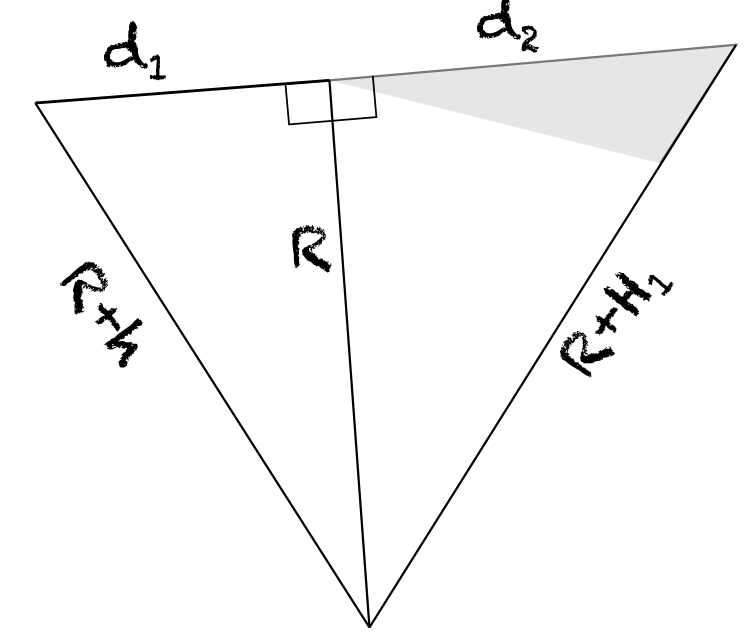
Y ya sabemos que podemos usar el teorema de Pitágoras para escribir una relación entre
todas las distancias involucradas:
\begin{align}
d_1^2 &= (R + h)^2 - R^2 = 2Rh + h^2 \
{\rm y}\
d_2^2 &= (R + H_1)^2 - R^2 = 2RH_1 + H_1^2 \
\end{align}
Sabiendo la distancia en línea recta \(D\) (que entre Chicago y Michigan City es de 60 km), lo que nos falta saber es la altura escondida por la curvatura terrestre \(H_1\). De las fórmulas anteriores, podemos derivar que \begin{align} H_1^2 &= R + \sqrt{R^2+(D-d_1)^2} \end{align}
Finalmente, lo único que nos falta es calcular el tamaño aparente o tamaño angular de los objetos a medida que nos alejamos. En la fotos de Chicago mostradas al principio de este post, la extensión horizontal \(s\) cubierta por la imagen es de 3 a 4 kilómetros. De nuestro post anterior, sabemos que el tamaño angular (llamémoslo \(\Delta\)) is inversamente proporcional a la distancia y proporcional al tamaño físico real: $$ \tan \Delta = \frac{s}{D} $$
La distancia del planetario Adler al centro de Chicago en línea recta es algo menos que 3 kilómetros, así que $$ \Delta_{\rm (desde~Adler)} \approx 45^\circ~$$
es decir, la ciudad cubre un cuarto de nuestro campo de visión a esta distancia (recordemos que, de oreja a oreja hay 180 grados).
Ahora, Michigan City se encuentra a 60 km de Chicago cruzando el lago, en ese caso, el tamaño aparente de la ciudad es de solamente $$ \Delta_{\rm (desde~Michigan)} \approx 2.5^\circ~$$
o sea, mucho más chico que nuestro campo de visión, pero aún así aproximadamente 5 veces más grande que el Sol (en la dirección horizontal no más!).
Ahora que tenemos las fórmulas necesarias para calcular \(H_1\) y \(\Delta\), lo podemos hacer para una representación clip-art de la ciudad de Chicago como ésta:
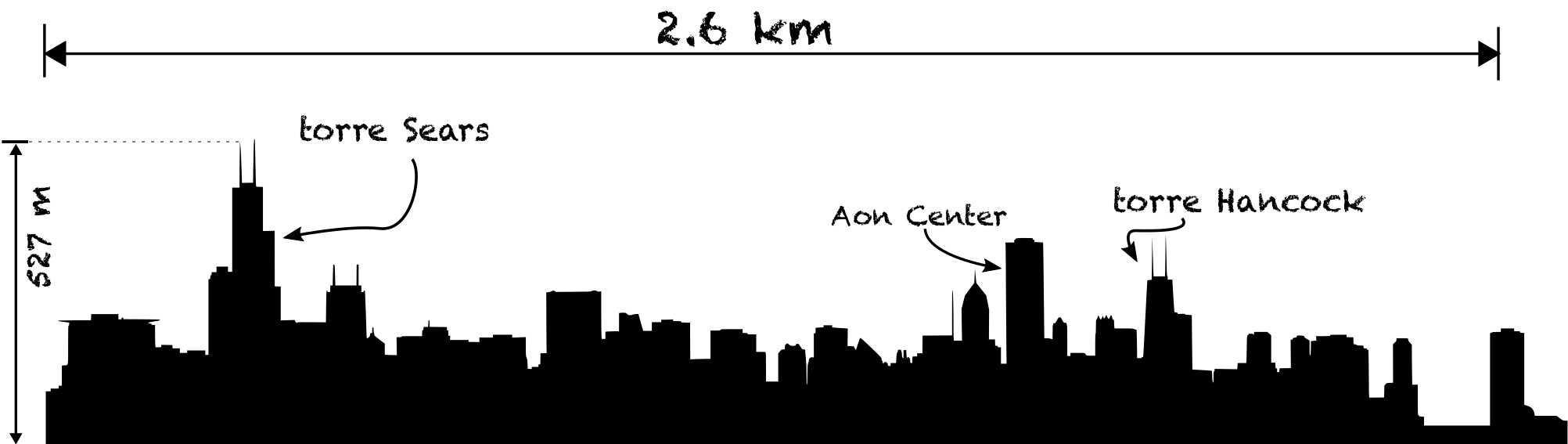
Podemos ver que la representación está un poco desactualizada, pero los principales rascacielos se pueden identificar claramente. Para nuestros propósitos prácticos, consideraremos que Chicago es un rectángulo con una altura 527 m (la altura de la Torre Sears, con las antenas) y de 2.8 km de ancho. Con éstos números, y nuestra altura (digamos \(h=1.75~\)m) podemos calcular \(H_1\) y \(\Delta\) para distintos valores de la distancia \(D,\) y ver cómo Chicago se va achicando y hundiendo!
Calculando cómo se ve Chicago desde Michigan City
He calculado el tamaño aparente y el hundimiento por debajo del horizonte de la ciudad de Chicago para cuatro distancias distintas: 10 km, 20 km, 40 km y 60 km. Esta última es la distancia a Michigan City.
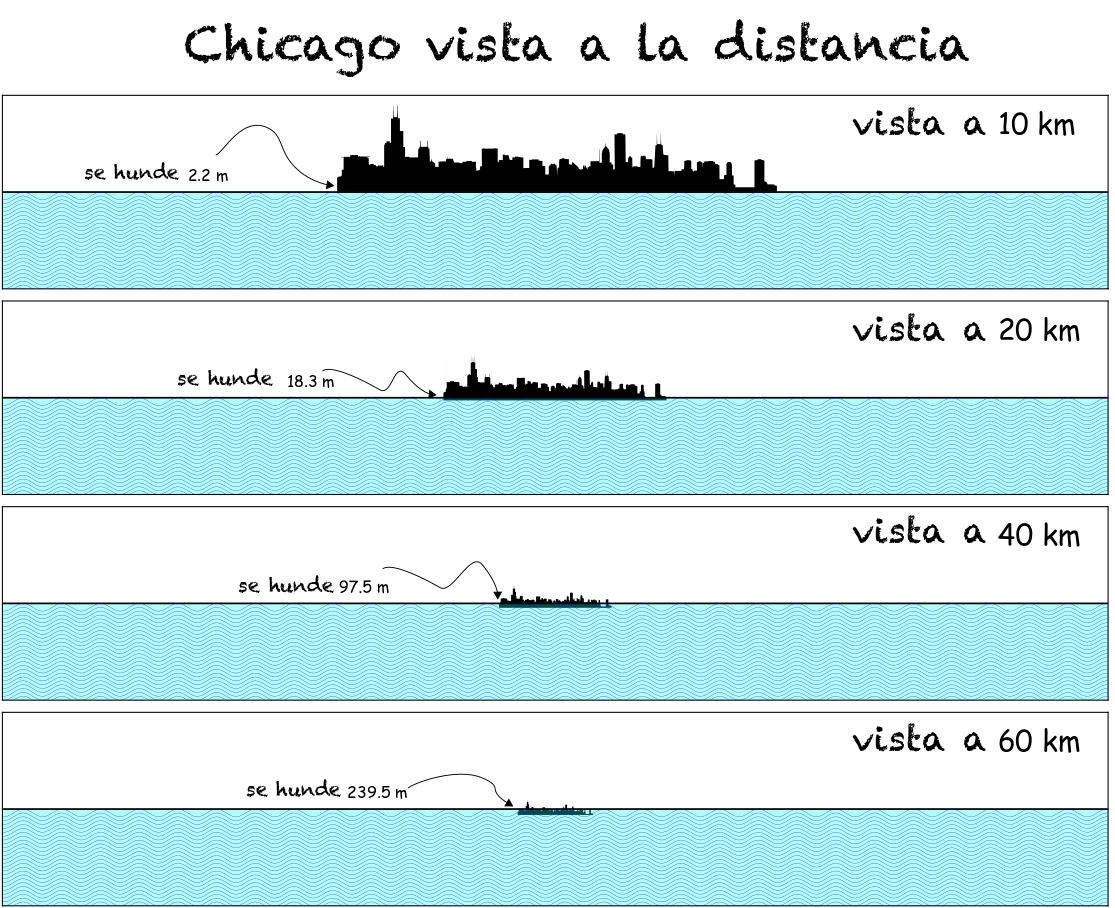
Enfoquémonos en el último ejemplo (60 km de distancia). En este caso, el hundimiento es \(H_1=240~\)m, es decir, casi la mitad \((46\%)\) de la ciudad de Chicago se encuentra por debajo del horizonte! Y sólo los edificios más altos se pueden ver.
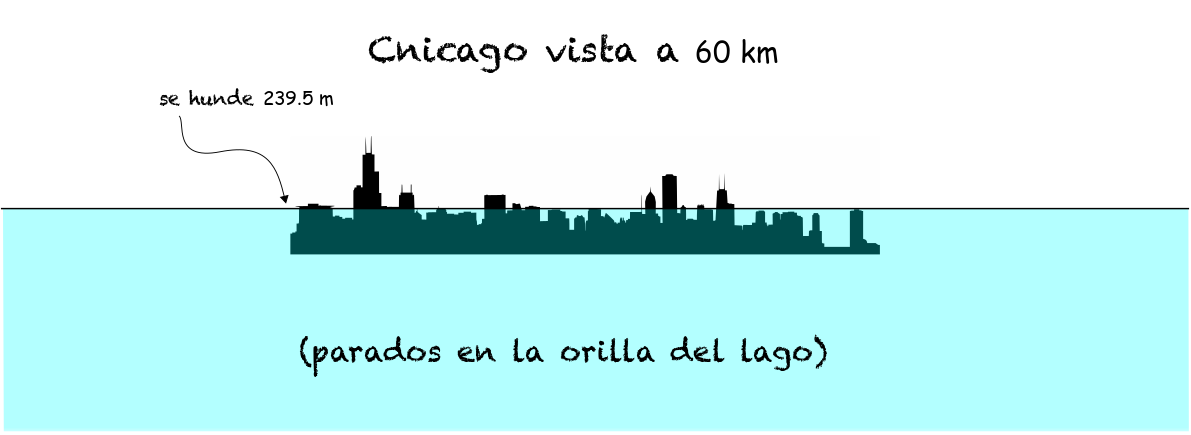
Ahora, aclaremos algo. Para este cálculo yo usé \(h=1.75~\)m, lo que implica que el observador está a la orilla del lago en Michigan City (casi mojándose los pies) observado la ciudad. Si es que, en lugar de la orilla del lago, el observador se encontrara en una calle aledaña a la playa (o un segundo piso de alguna casa cercana), la altura \(h\) sería mayor. Como ejemplo, supongamos que los pies del observador están a más de 6 metros de altura (en total, \(h=8~\)m). Entonces, la visión de Chicago será así:
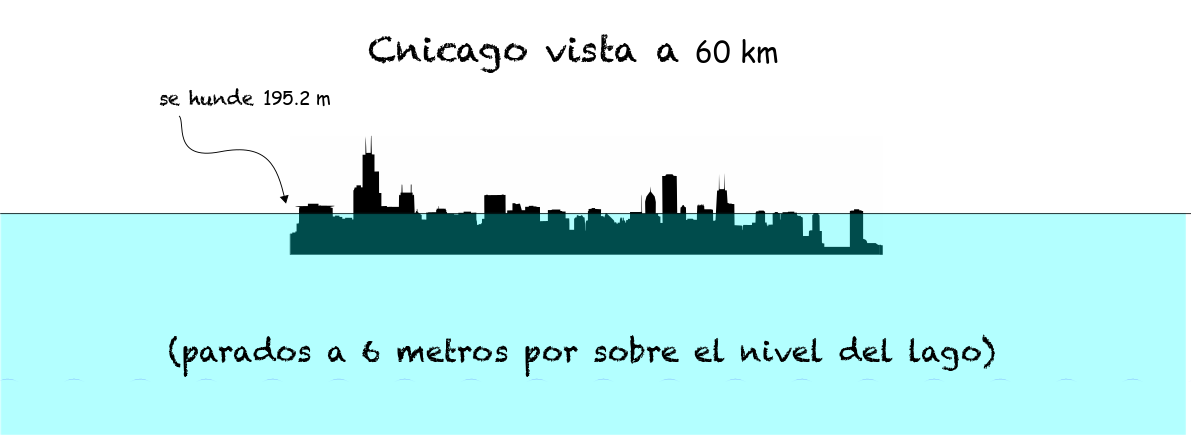
La diferencia es menor (el hundimiento ahora es \(H_1=195~\)m), pero importante, ya que muchos edificios tienen alturas de aproximadamente 200 metros, entonces, al reducir \(H_1\) de 240m a 195m, estos edificios comienzan a aparecer en el horizonte.
Fotos tomadas desde Michigan City
Michigan City es ideal para apreciar los efectos la curvatura de la Tierra, no sólo porque se encuentra en oposición a Chicago, si no también porque hay una infinitud de fotos en Internet. Es en especial importante el hecho que de Michigan City tiene un punto de referencia: el faro en la costa (ver imagen de Google maps abajo). Este faro te da una referencia clara respecto de la orientación del fotógrafo al momento de capturar la imagen, así como una idea de la altura a la que fue tomada.
Entonces, cómo andan nuestros cálculos?
La siguiente imagen de Imgur está tomada my cerca del agua, como pueden ver por la cercanía al faro. Uno puede contar 8 o 10 edificios, aunque sólo 4 sobresalen claramente. Estos 4 rascacielos son, de izquierda a derecha: Sears Tower, Aon Center, Trump Tower, y al final Hancock Center.
Chicago skyline this summer, from Michigan City, IN at sunset
Qué pasa si la foto está tomada a una altura ligeramente mayor? Consideremos esta imagen de Reddit tomada en la misma zona (ahí está el faro), pero a una altura mayor (se puede ver gente en la playa). Los edificios son casi los mismos, pero aparecen otros de menor altura.
downtown chicago from indiana from r/chicago
Finalmente, podemos encontrar una imagen en Imgur tomada a varios metros por sobre el nivel del lago. Ahora muchos edificios aparecen, aunque casi todos los edificios de baja altura aún están por debajo del horizonte.
Chicago Skyline from Michigan City, Indiana.
Con eso terminamos este (largo) post! Con una serie de fotos y simples cálculos, hemos demostrado cómo la curvatura de la Tierra es apreciable a simple vista a 60 kilómetros de distancia.