Punto de Fuga
La línea del horizonte se encuentra a una distancia enorme (“infinita”)? O simplemente a sólo algunos kilómetros de distancia? Cuál es la relación entre el horizonte y el punto de fuga?
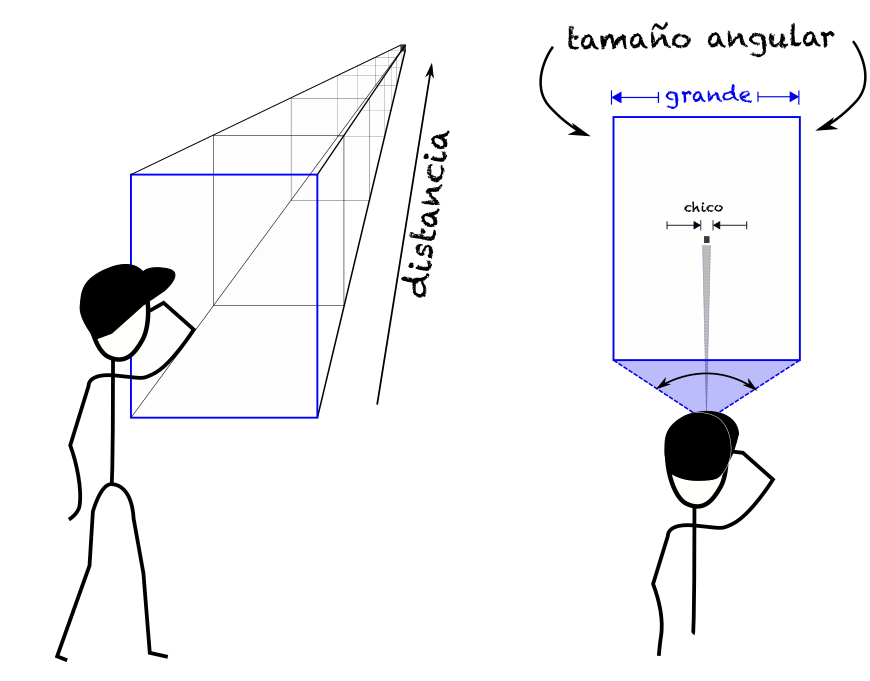
Todos sabemos que a medida que un objeto se aleja, se ve más pequeño. El objeto no ha cambiado en sí. Es el tamaño angular que éste cubre en nuestro campo de visión el se reduce con la distancia (ver siguiente figura ilustrando este efecto). Uno puede extrapolar este hecho y afirmar que, a medida que el objeto se va “hacia el infinito”, su tamaño angular se reducirá a cero. Cuando el objeto se reduce a un punto, la ubicación de éste es conocida como el punto de fuga.
La geometría básica detrás del concepto de punto de fuga sirve como herramienta esencial en la ilustración de perspectiva tridimensional. Esta técnica es de conocimiento común para diseñadores, artistas y arquitectos. Para representar la perspectiva del observador en el papel, uno utiliza el infinito, posicionándolo en algún punto del cuadro, generando líneas rectas (paralelas en el mundo 3D, pero convergentes en la proyección 2D) a partir de ese punto de origen.
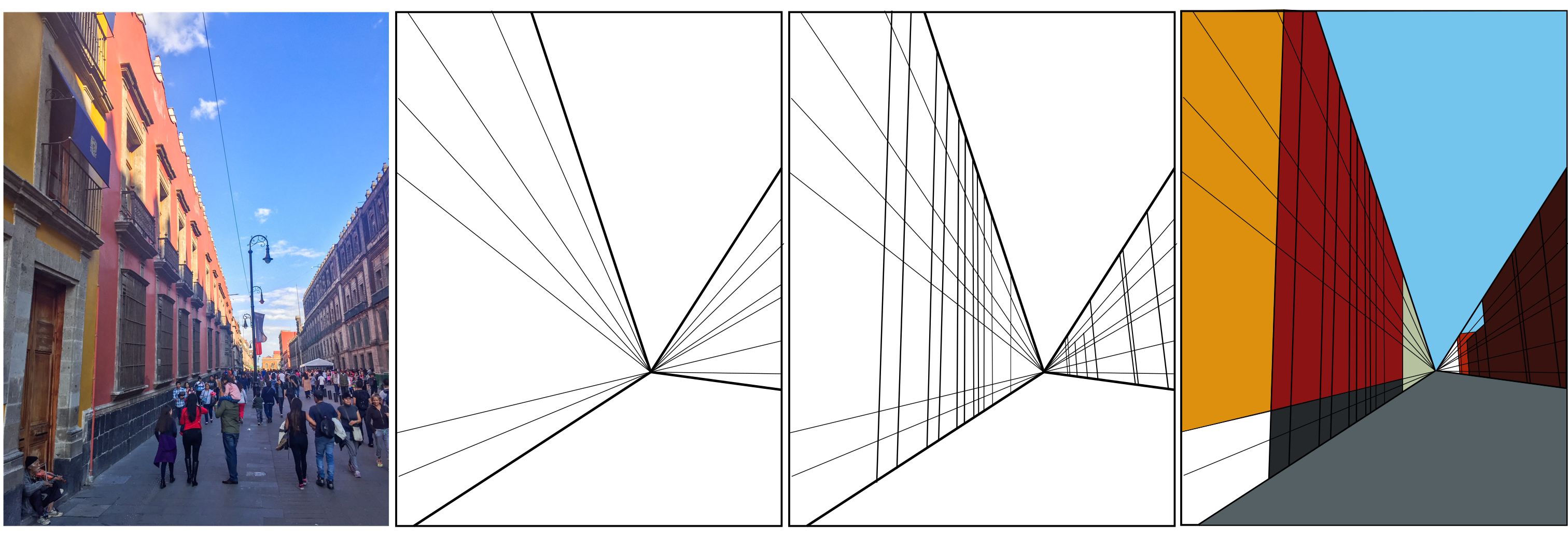
Como ejemplo, he usado una foto que tomé en Noviembre de 2017 en ciudad de México, cerca del Zócalo (ver figura). Primero, uno identifica la ubicación del punto de fuga en la imagen, y luego traza líneas rectas a partir de ese punto (segundo panel). Uno puede incluir trazos adicionales que representan las líneas que son verticales en el espacio 3D real (tercer panel), para finalmente asignar colores que separen las distintas estructuras (cuarto panel).
El Horizonte y el Infinito
Cuál es la relación entre estos conceptos y la línea del horizonte? Es la desaparición de barcos en el horizonte un efecto de la curvatura de la Tierra, o una consecuencia de la distancia, similar a la de punto de fuga?
Pues bien, la diferencia entre mirar al infinito y mirar al verdadero horizonte es muy clara cuando el observador se encuentra sobre superficies de radio de curvatura pequeño (es decir, sobre una esfera pequeña). La siguiente figura ilustra esta diferencia.
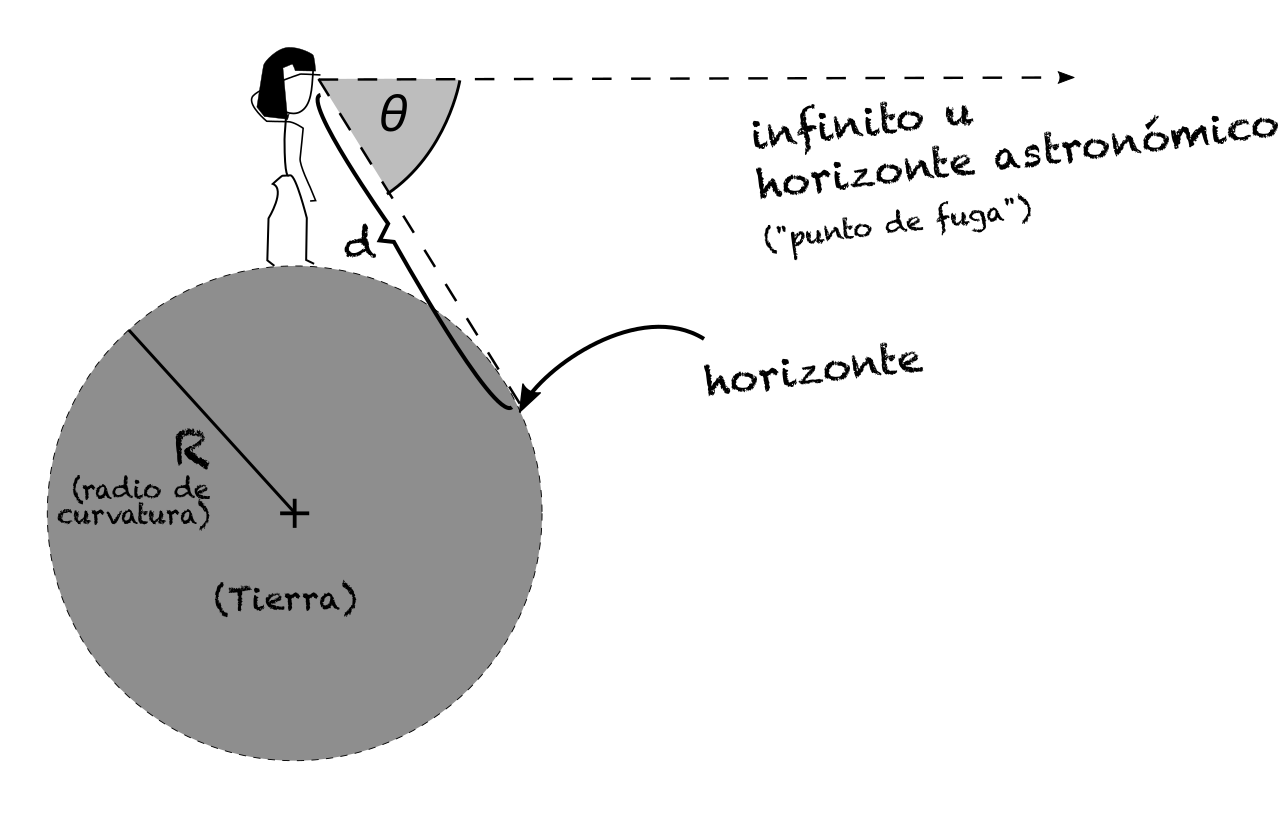
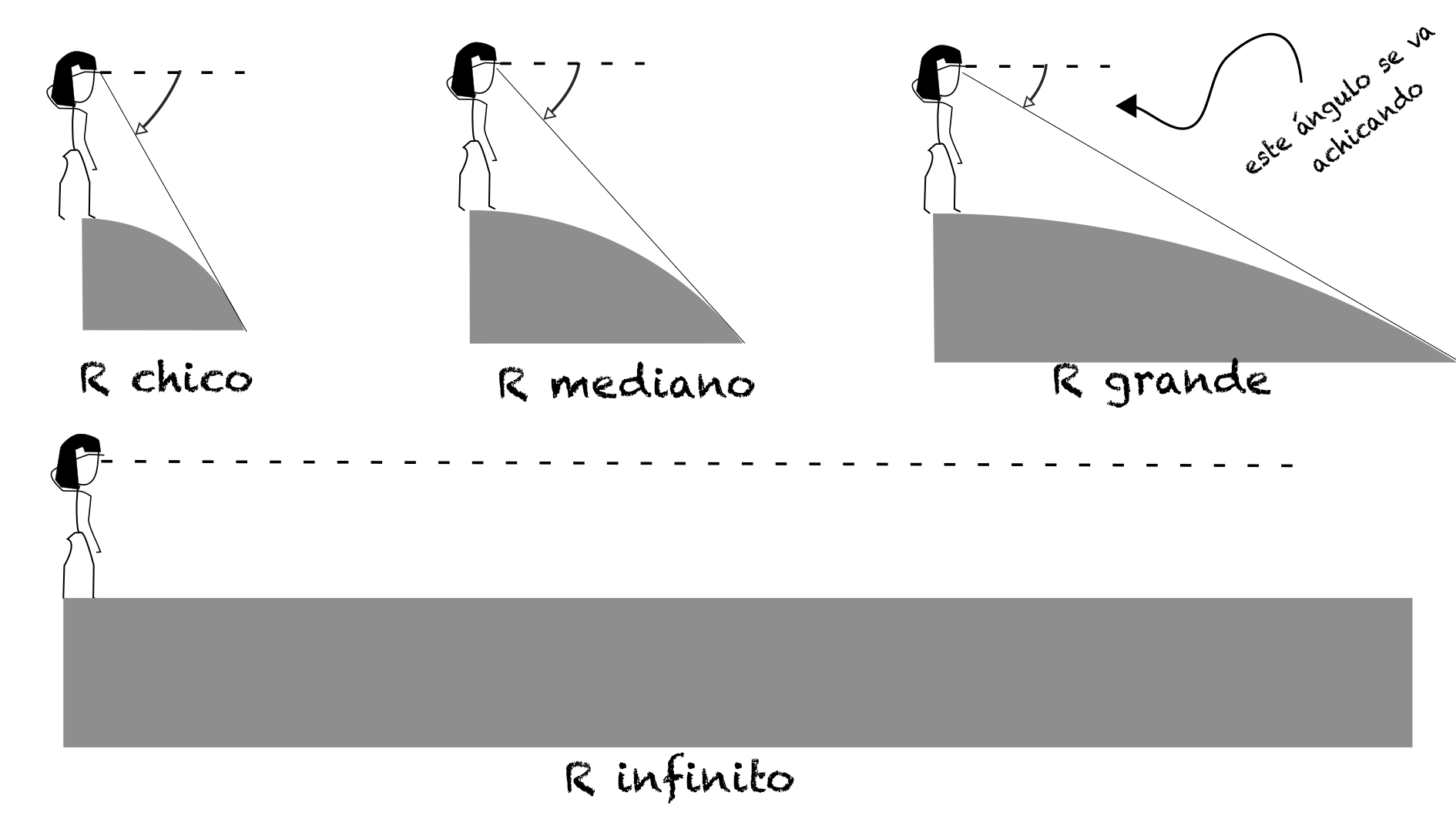
A medida que el radio de curvatura \(R\) crece (es decir, el tamaño de la esfera sobre la que estamos parados aumenta), el ángulo \(\theta\) se reduce. Cuando el radio \(R\) is infinito – lo que equivale a decir que la superficie sobre la que estamos parados es plana – entonces \(\theta=0^\circ\). Es decir, si uno viviera sobre un plano infinito (o el radio de curvatura \(R\) is infinito), el el horizonte siempre estaría a nivel de los ojos, como se ilustra en la siguiente figura, sin importar la altura del observador.
El Cálculo
Ahora que tenemos los principios básicos a la mano, calculemos la diferencia entre el punto de fuga, y el horizonte debido a la curvatura. Es una diferencia apreciable a simple vista?
Veamos. Ya sabemos que el infinito está a un ángulo de cero grados (\(0^\circ\)) por debajo de la línea de visión horizontal. A cuántos grados por debajo de la línea de visión está el horizonte?
Si el radio de la Tierra is de aproximadamente 6400 km y tú mides 1.75 metros, entonces, por trigonometría básica (ver siguiente figura), el horizonte se encuentra a una distancia \(d\)
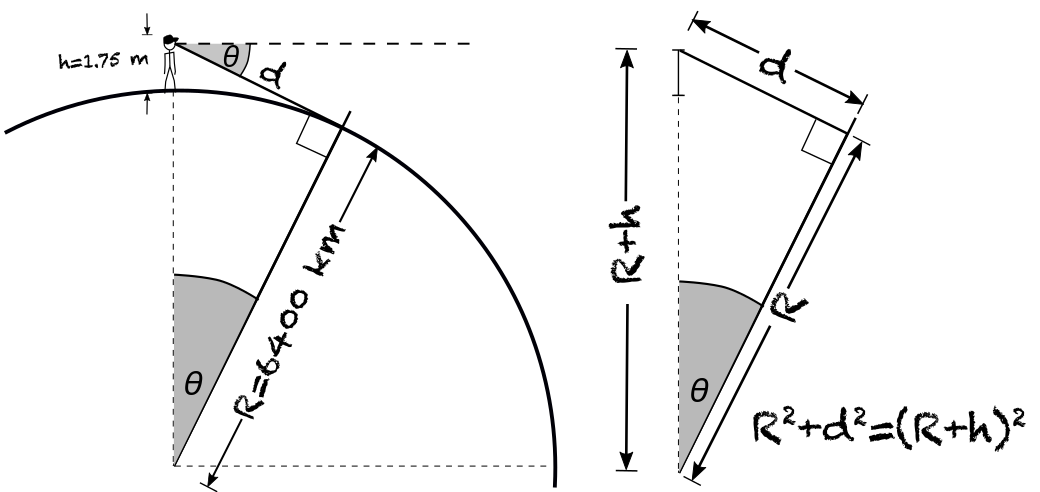
Usando el teorema de Pitágoras, podemos concluir que esta distancia al horizonte (\(d\)) satisface la fórmula
\begin{align}
d^2 &= (R + h)^2 - R^2 = 2Rh + h^2 \
{\rm o\;sea}\
d &= \sqrt{2\times6400000\times1.75 + 1.75^2}~{\rm metros} = 4732~{\rm metros}
\end{align}
Es decir, el horizonte se encuentra sólo 5 kilómetros de distancia!! Por supuesto, esto es asumiendo la ausencia de obstáculos (montañas, árboles, edificios), por lo que representa la realidad en lugares con muy poco relieve o a la orilla del mar.
Ahora, lo que nos interesa es ese ángulo \(\theta\). De nuevo, usando el triángulo rectángulo en la figura anterior, sabemos que existe una relación entre los lados del triángulo y una propiedad de \(\theta\) conocida como el coseno: $$ \cos\theta = \frac{R}{R+h} $$
Usando, como antes, \(R=6400\) km y \(h=1.75\) m, tenemos que el ángulo es $$ \theta = 0.04^\circ $$
Es decir, la diferencia entre mirar directo al infinito (a la altura de los ojos) y mirar el horizonte en el mar, es de sólo 0.04 grados. Apreciar esta diferencia a simple vista (sin instrumentos) no es fácil. La resolución angular promedio del ojo humano es cerca de 0.02 grados por lo que somos apenas capaces físicamente de notar esta diferencia. Para que el horizonte baje, digamos, un grado completo, por debajo de la línea horizontal, tendríamos que ir mucho más alto. Reemplazando \(\theta=1^\circ\) en la formula anterior, encontramos que la altura necesaria es de \(h=975\) metros! Lo que supera la altura del edificio más alto del mundo. Esta dificultad puede ser superada por el experimento descrito a continuación.
El Experimento
Observemos el atardecer sentados sobre la playa y lo más cercanos a la orilla como sea posible. Digamos que, sentados de tal forma, la altura de nuestro ojos sobre el nivel del mar es de apenas 40 cm. Usando las mismas dos formulas de arriba, la distancia al horizonte y el ángulo por debajo de la horizontal son, respectivamente \(d=\)2.3 km y \(\theta=0.02^\circ\). Esperemos a que el Sol se oculte completamente. Apenas esto ocurra, pongámonos de pie rápidamente, y retrocedamos algunos pasos alejándonos de la orilla (y subiendo un poco nuestra elevación). Digamos que ahora nuestros ojos están a 2.5 m por sobre el nivel del mar: entonces \(d=\)5.7 km y \(\theta=0.05^\circ\). Ahora podemos ver \(0.03^\circ\) más por debajo de la horizontal que estando sentados!!
Con este pequeño ángulo extra, parte del Sol (que ya se había puesto) será nuevamente visible (por muy poco). Es esta diferencia apreciable? Bueno, el Sol tiene un tamaño angular de \(0.5^\circ\), es decir, con \(0.03^\circ\) podemos ver un 8% del diámetro del Sol. Es poco, pero lo suficiente como para ver una franja de luz (en este caso, lo que importa es la cantidad de luz, más que el tamaño angular), la cual es visible porque estamos mirando desde mayor altura, corriendo el horizonte hacia abajo, lo que ocurre debido a la curvatura de la Tierra.